Examples of grid construction

In addition to the already discussed construction of Cartesian grid using dune.grid.structuredGrid and dune.grid.cartesianDomain and the usage of dictionaries discussed in the general concepts section, it is also possible to read grid files using either the DGF or gmsh format (or other formats available through the meshio package).

import numpy
from matplotlib import pyplot
from dune.alugrid import aluSimplexGrid as leafGridView
from dune.grid import OutputType, reader
from dune.fem.space import lagrange as solutionSpace
from dune.fem.scheme import galerkin as solutionScheme
from ufl import TestFunction, TrialFunction, SpatialCoordinate
from ufl import dx, grad, grad, dot, inner, conditional, sin

Example using the Dune Grid Format (DGF)

Please read the Dune Grid Format (DGF) for a detailed description of DGF. The format works for 2d or 3d and most DUNE grids can be constructed using a DGF file. The format allows easy description of boundary ids (see below) and parameters. See the section about boundary conditions to learn how to use these in a weak form.

Note

The DGF is ASCII based and thus only meant for prototyping and testing. For serious computations use meshio or the pickling approach.

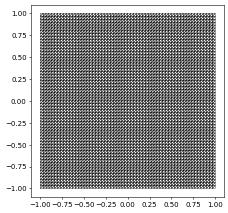
domain2d = (reader.dgf, "triangle.dgf")

# specify dimgrid since it cannot be easily extracted from the dgf file
aluView = leafGridView(domain2d, dimgrid=2)
aluView.plot(figsize=(5,5))

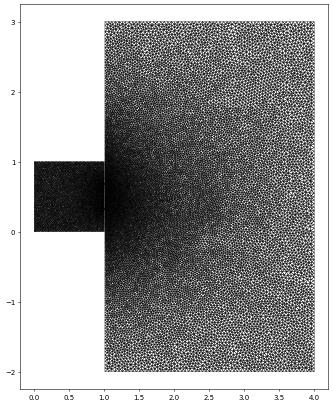
There is also a reader.gmsh option allowing previously stored gmsh files to be read. The grid is the one used in the wave equation example.

waveDomain = (reader.gmsh, "wave_tank.msh")
waveGrid = leafGridView(waveDomain, dimgrid=2)
waveGrid.plot(figure=pyplot.figure(figsize=(10,10)))

3D example (using PyGmsh)

In this example we use pygmsh to construct a tetrahedral mesh and solve a simple Laplace problem. The following code is taken from the pygmsh homepage.

try:
    import pygmsh
    with pygmsh.geo.Geometry() as geom:
        poly = geom.add_polygon([
              [ 0.0,  0.5, 0.0], [-0.1,  0.1, 0.0], [-0.5,  0.0, 0.0],
              [-0.1, -0.1, 0.0], [ 0.0, -0.5, 0.0], [ 0.1, -0.1, 0.0],
              [ 0.5,  0.0, 0.0], [ 0.1,  0.1, 0.0] ], mesh_size=0.05)
        geom.twist(
            poly,
            translation_axis=[0, 0, 1], rotation_axis=[0, 0, 1], point_on_axis=[0, 0, 0],
            angle=numpy.pi / 3,
        )
        mesh = geom.generate_mesh(verbose=False)

    points, cells = mesh.points, mesh.cells_dict
    domain3d = {"vertices":points.astype("float"), "simplices":cells["tetra"]}
except ImportError: # pygmsh not installed - use a simple cartesian domain
    print("pygmsh module not found using a simple Cartesian domain - ignored")
    from dune.grid import cartesianDomain
    domain3d = cartesianDomain([-0.25,-0.25,0],[0.25,0.25,1],[30,30,60])

gridView3d  = leafGridView(domain3d)
space3d = solutionSpace(gridView3d, order=1)

u = TrialFunction(space3d)
v = TestFunction(space3d)
x = SpatialCoordinate(space3d)
scheme3d = solutionScheme((inner(grad(u),grad(v))+inner(u,v))*dx ==
                        conditional(dot(x,x)<.01,100,0)*v*dx,
                        solver='cg')

uh3d = space3d.interpolate([0],name="solution")
scheme3d.solve(target=uh3d)
# note: plotting with matplotlib not yet available for 3d grids
gridView3d.writeVTK('3dexample', pointdata=[uh3d],
                    outputType=OutputType.appendedraw)

Converting gmsh to DGF

Using the above convenient way of generating grids in Python we can then store those as DGF which allows to add boundary ids of vertex and element parameters in a simple way. Use gmsh2DGF from gmsh2dgf to convert the above points and cells to a string which can be read by reader.dgfString.

from gmsh2dgf import gmsh2DGF
from dune.grid import reader

dgf = gmsh2DGF(points, cells)
domain3d = (reader.dgfString, dgf)
gridView3d  = leafGridView(domain3d, dimgrid=3)

Tip

Store the DGF mesh to a file for later reuse with reader.dgf, see above.

with open ("3dmesh.dgf", "w") as file:
    file.write(dgf)

Attaching boundary ids to a grid constructed with gmsh using DGF

The Dune Grid Format (DGF) allows to either specify BoundarySegments or a BoundaryDomain. Boundary segments require to specify a boundary id for a selection of intersections of an element with the boundary, e.g. a collection of edges of triangles located on the boundary. For testing and prototyping it is very convenient to use the boundary domain approach instead, where for each boundary id (short: bnd id) a bounding box is described and each boundary segment that is found inside this box is assigned the bnd id. This approach also allows to specify a default value which is assigned to all segments not found in any of the specified boxes. This approach works in 2d as well as 3d.

Tip

Specify the bounding box for simple boundaries such as outer walls and straight lines and surfaces and use the default value to mark a particularly complex boundary in the interior.

try:
    with pygmsh.occ.Geometry() as geom:

        # Define domain
        L = 1; H = 1
        # circles
        c = 0.2; r = 0.05

        # Grid size function
        def size(dim, tag, x, y, z, lc):
            resolution = 0.06
            d = ((x - c)**2 + (y - c)**2)**0.5
            if d < 3 * r:
                return 0.25*resolution

            d = ((x - (1-c))**2 + (y - (1-c))**2)**0.5
            if d < 3 * r:
                return 0.25*resolution

            # default is a coarser mesh
            return resolution

        # create rectangle and circles
        rectangle = geom.add_rectangle([0, 0, 0], L, H)
        obs1 = geom.add_ball([c, c, 0], r)
        obs2 = geom.add_ball([1-c, 1-c, 0], r)
        # subtract the two obstacles from the volume to create holes
        geom.boolean_difference(rectangle, [obs1, obs2])
        geom.set_mesh_size_callback(size)
        mesh = geom.generate_mesh(dim=2)

        eps = 0.01 # tolerance
        # lower left circle min and max
        c1 = [c - r - eps, c + r + eps]
        # upper right circle min and max
        c2 = [(1-c) - r - eps, (1-c) + r + eps]

        # dictionary containing id and a list containing the lower left and upper right corner of the bounding box
        bndDomain = {1: [[-1.0 , -1.0 ], [0.0  , H+0.1]], # bounding box inflow
                     2: [[   L , -1.0 ], [L+1.0, H+0.1]], # bounding box outflow
                     4: [[c1[0], c1[0]], [c1[1], c1[1]]], # bounding box lower left circle
                     5: [[c2[0], c2[0]], [c2[1], c2[1]]], # bounding box upper right circle
                     3: "default"  # top and bottom wall,
                     # which are all other segments not contained in the above bounding boxes
                    }

        # return dgf string which can be read by DGF parser or written to file for later use
        dgf = gmsh2DGF(mesh.points, mesh.cells_dict, bndDomain=bndDomain, dim=2)
        domain2d = (reader.dgfString, dgf)
except ImportError: # pygmsh not installed - use a simple cartesian domain
    print("pygmsh module not found using a simple Cartesian domain - ignored")
    from dune.grid import cartesianDomain
    domain2d = cartesianDomain([-0.25,-0.25],[0.25,0.25],[30,30])

gridView2d = leafGridView(domain2d, dimgrid=2)

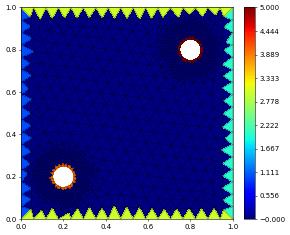
Visualizing Boundary Ids

After construction of a grid we can visualize boundary ids by assigning a piecewise constant function to hold the value of adjacent boundaries. This is not necessarily unique but works in most cases.

from gmsh2dgf import projectBoundaryIds

bndIds = projectBoundaryIds( gridView2d )
bndIds.plot()

Using meshio to read a gmsh file

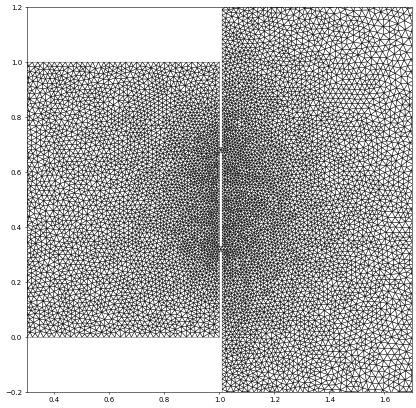
We will use the meshio package to read a gmsh file, extract the points and cells and use that to construct a Dune grid. The final part is then quite similar to the above. We use the 2D grid from the wave equation test case. Note that this is a 2D grid but the points are returned as 3D points so we need to remove the final columns containing only zeros. We have already seen this grid above so let’s zoom in to the ‘slit’ region…

Todo

Add a way to describe boundary data when using meshio.

try:
    import numpy as np
    import meshio
    mesh = meshio.read("wave_tank.msh")
    points = np.delete( mesh.points, 2, 1) # remove the z component from the points
    cells = mesh.cells_dict
    waveDomain = {"vertices":points.astype("float"), "simplices":cells["triangle"]}
    waveGrid = leafGridView(waveDomain)
    waveGrid.plot(figure=pyplot.figure(figsize=(10,10)),xlim=[0.3,1.7],ylim=[-0.2,1.2])
except ImportError:
    print("This example requires the meshio package which can be installed using pip.")

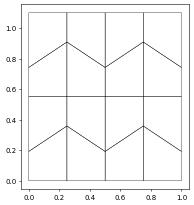
Here is a second example where we want to read a gmsh containing quadrilateral elements. Note that the vertices of the cells are ordered counterclockwise which is not identical to the ordering required by the Dune reference element. The last two vertices need to be exchanged:

if meshio:
    from dune.alugrid import aluCubeGrid
    mesh = meshio.read("quads.msh")
    points2d = np.delete(mesh.points,2,1)
    cells = mesh.cells_dict['quad']
    cells[:, [2, 3]] = cells[:, [3, 2]]
    domain = {"vertices":points2d, "cubes":cells}
    quadGrid  = aluCubeGrid(domain)
    quadGrid.plot()

1D example

It’s also possible to create grids in 1D

from dune.grid import onedGrid
v = [numpy.log(i) for i in range(1,100)]
e = [(i,i+1) for i in range(1,len(v))]
g = onedGrid(constructor={"vertices":v, "simplices":e})
s = solutionSpace(g)
x = SpatialCoordinate(s)
u = s.interpolate(sin(x[0]), name="u")
u.plot()

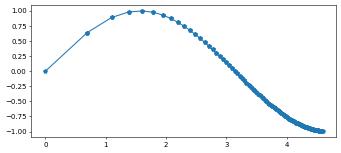
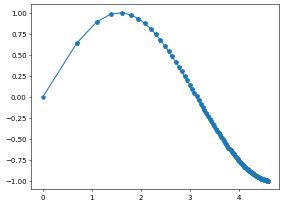
pyplot can very easily be used in 1d using the tessellate method on the grid which will be described in more detail in the section about the bindings for the full dune grid interface.

pyplot.plot(g.tessellate()[0], u.pointData(), '-p')

[<matplotlib.lines.Line2D at 0x7f601014fe50>]

This page was generated from the notebook othergrids_nb.ipynb and is part of the tutorial for the dune-fem python bindings