Backup and restore (pickling)

We show here how the state of a simulation can be stored and restored using pickle. This is still work in progress and based on an extension of the standard pickle module available in dune.common:

import dune.common.pickle

Let’s first construct a grid and some discrete function:

import numpy
from dune.alugrid import aluConformGrid
from dune.fem.view import adaptiveLeafGridView as view
from dune.grid import cartesianDomain, Marker
from dune.fem.function import gridFunction
from dune.fem.space import lagrange
from dune.fem import adapt
from dune.ufl import Constant
import ufl

order = 4
def setup():
    gridView = view( aluConformGrid( cartesianDomain([-2,-2],[2,2],[10,10]) ) )

    @gridFunction(gridView, name="gf", order=3)
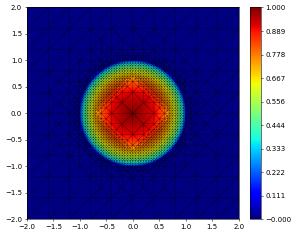
    def gf(x): return numpy.sqrt(1-(x[0]**2+x[1]**2)) if x[0]**2+x[1]**2<1 else 0

    space = lagrange(gridView, order=order)
    df = space.interpolate(gf,name="test")

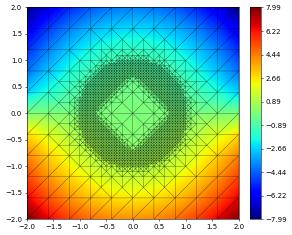
    gridView.hierarchicalGrid.globalRefine(4)
    for i in range(5):
        gridView.hierarchicalGrid.mark(lambda e:
             Marker.refine if df.localFunction(e).jacobian([1./3.,1./3.]).infinity_norm > 1
             else Marker.coarsen)
        adapt(gridView.hierarchicalGrid)
        df.interpolate( gf )
    print("size of adapted grid view:", gridView.size(0))

    t = Constant(0,"time")
    x = ufl.SpatialCoordinate(space)
    gf = gridFunction(ufl.tanh(2*(t*x[0]-x[1]))*ufl.dot(x,x),
                     gridView,order=2,name="tanh")
    return df, space.interpolate(gf,name="tanh_h"),gf

Pickling

dune.common provides a pickle module with a similar functionality as Python pickle. In fact pickle.dump can be used to (un)pickle many dune objects. The dune.common.pickle module adds the JIT generation of modules on load so that pickled data can be recreated on machines where these JIT modules have not yet been generated. In addition an dune.common.pickle.SeriesPickler is available which can for example be used to pickle time series data.

Let’s first write a function that dumps some discrete functions:

def dump():
    df1, df2, gf = setup()

    with open("test.dbf","wb") as f:
        dune.common.pickle.dump([df1,df2],f)

    series = dune.common.pickle.SeriesPickler("test", objects=[df1,df2])

    tsps = [0,0.4,0.8,1.2,2.5,5]
    def inCircle(p,t):
        p -= [numpy.cos(t),numpy.sin(t)]
        return p.two_norm < 0.3
    for i,tsp in enumerate(tsps):
        for i in range(3):
            df1.gridView.hierarchicalGrid.mark(lambda e:
                 Marker.refine if inCircle(e.geometry.center,tsp)
                 else Marker.keep)
            adapt([df1,df2])
        gf.time = tsp
        df2.interpolate(gf)
        series.dump({"time":tsp})
dump()

size of adapted grid view: 4288

Now we can reconstructed the data again:

with open("test.dbf","rb") as f:
    df1,df2 = dune.common.pickle.load(f)
df1.plot()

series = dune.common.pickle.SeriesPickler("test")
while True:
    try:
        data, df = series.load()
    except FileNotFoundError:
        break
    print(data)
    df[1].plot()

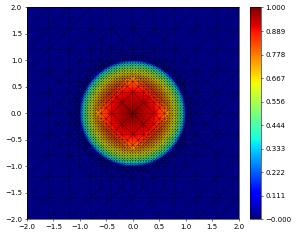
{'time': 0, 'dumpFileName': 'test.000000.dbf'}

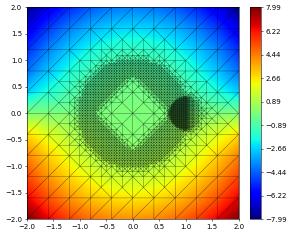
{'time': 0.4, 'dumpFileName': 'test.000001.dbf'}

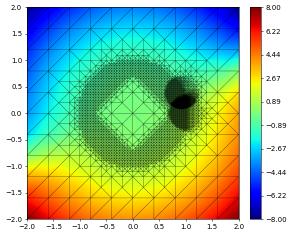
{'time': 0.8, 'dumpFileName': 'test.000002.dbf'}

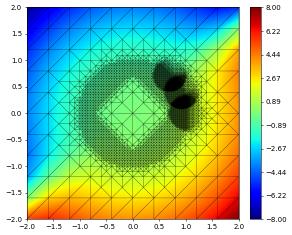
{'time': 1.2, 'dumpFileName': 'test.000003.dbf'}

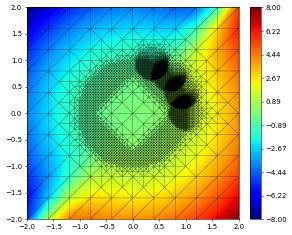
{'time': 2.5, 'dumpFileName': 'test.000004.dbf'}

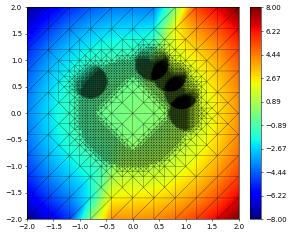
{'time': 5, 'dumpFileName': 'test.000005.dbf'}

A Chekpointer class

In the code below, we implement a class that stores a hierarchical grid and some discrete functions and other information and can serve a starting point for pickling data for complex simulations. This example relies on the original pickle module.

import pickle
class CheckPointer:
    # if 'gridView=None' then restore grid view using given file name
    # otherwise backup 'gridView' to given file
    def __init__(self,fileName,gridView=None):
        if gridView is None: # restore file
            self.file = open(fileName,'rb')
            self.gridView = pickle.load(self.file)
        else:             # store file
            self.file = open(fileName,'wb')
            self.gridView = gridView
            pickle.dump(self.gridView,self.file)
        self.items = []

    # add an item to pickle when backup is called (or restore)
    def add(self,item):
        assert hasattr(item,"write") and hasattr(item,"read")
        self.items += [item]

    def backup(self):
        pickle.dump([i.write() for i in self.items], self.file)
    def restore(self):
        for i,d in zip(self.items, pickle.load(self.file)):
            i.read(d)

First test: construct the grid view, some discrete function, and refine the mesh. The result is then store in a file.

def test1(fileName):
    df1, df2,_ = setup()
    checkPointer = CheckPointer(fileName, df1.gridView)
    checkPointer.add(df1)
    checkPointer.add(df2)
    checkPointer.backup()

test1("dump.pickle")

size of adapted grid view: 4288

Now we restore the backup

checkPointer = CheckPointer("dump.pickle")
gridView = checkPointer.gridView
print("size of restored grid view:", gridView.size(0))
space = lagrange(gridView, order=order)
df1 = space.function(name="test")
df2 = space.function(name="test")
checkPointer.add(df1)
checkPointer.add(df2)
checkPointer.restore()
df1.plot()
df2.plot()

size of restored grid view: 4288

This page was generated from the notebook backuprestore_nb.ipynb and is part of the tutorial for the dune-fem python bindings