Mean Curvature Flow (revisited)
As discussed before we can simulate the shrinking of a sphere under mean curvature flow using a finite element approach based on the following time discrete approximation: \begin{align} \int_{\Gamma^n} \big( U^{n+1} - {\rm id}\big) \cdot \varphi + \tau \int_{\Gamma^n} \big( \theta\nabla_{\Gamma^n} U^{n+1} + (1-\theta) I \big) \colon\nabla_{\Gamma^n}\varphi =0~. \end{align} Here \(U^n\) parametrizes \(\Gamma(t^{n+1})\) over \(\Gamma^n:=\Gamma(t^{n})\), \(I\) is the identity matrix, \(\tau\) is the time step and \(\theta\in[0,1]\) is a discretization parameter.
If the initial surface \(\Gamma^0\) is a sphere of radius \(R_0\), the surface remains sphere and we have an exact formula for the evolution of the radius of the surface
To compare the accuracy of the surface approximation we compute an average radius of the discrete surface in each time step \(t^n\) using
Computing \(R_h^n\) requires a grid traversal and a number of calls to interface methods on each element. Doing this on the Python side has a potential performance impact which we investigate here by comparing a pure python implementation with a hybrid approach where computing \(R_h^n\) is implemented in C++ using the dune.generator.algorithm functionality.
[1]:
import time, io
import pickle
import numpy
from matplotlib import pyplot as plt
from matplotlib.ticker import ScalarFormatter
from ufl import *
import dune.ufl
from dune.generator import algorithm
import dune.geometry as geometry
import dune.fem as fem
def plot(ct, ct2):
fig, ax = plt.subplots()
plt.loglog(ct[0][:], ct[1][:],'*-', markersize=15, label='hybrid')
plt.loglog(ct2[0][:], ct2[1][:],'*-', markersize=15, label='python')
plt.grid(True)
for axis in [ax.xaxis, ax.yaxis]:
axis.set_major_formatter(ScalarFormatter())
axis.set_minor_formatter(ScalarFormatter())
yticks = ax.yaxis.get_minor_ticks()
for t in yticks:
t.label1.set_visible(False)
xticks = ax.xaxis.get_minor_ticks()
for t in xticks:
t.label1.set_visible(False)
plt.yticks(numpy.append(ct[1], ct2[1]))
plt.xticks(ct[0])
plt.legend(loc="upper left")
plt.xlabel('Number of Grid Elements (log)',fontsize=20)
plt.gcf().subplots_adjust(bottom=0.17, left=0.16)
plt.ylabel('Runtime in s (log)',fontsize=20)
# polynomial order of surface approximation
order = 2
# initial radius
R0 = 2.
# end time
endTime = 0.1
Main function for calculating the mean curvature flow of a given surface. If first argument is True the radius of the computed surface is computed using an algorithm implemented in C++ otherwise the computation is done in Python.
[2]:
def calcRadius(surface):
R,vol = 0, 0
for e in surface.elements:
rule = geometry.quadratureRule(e.type, 4)
for p in rule:
geo = e.geometry
weight = geo.volume * p.weight
R += geo.toGlobal(p.position).two_norm * weight
vol += weight
return R/vol
code = """
#include <dune/geometry/quadraturerules.hh>
template< class Surface >
double calcRadius( const Surface &surface ) {
double R = 0, vol = 0.;
for( const auto &entity : elements( surface ) ) {
const auto& rule = Dune::QuadratureRules<double, 2>::rule(entity.type(), 4);
for ( const auto &p : rule ) {
const auto geo = entity.geometry();
const double weight = geo.volume() * p.weight();
R += geo.global(p.position()).two_norm() * weight;
vol += weight;
}
}
return R/vol;
}
"""
switchCalcRadius = lambda use_cpp,surface: \
algorithm.load('calcRadius', io.StringIO(code), surface) \
if use_cpp else calcRadius
Timings for a number of different grid refinements is dumped to disk
[3]:
from dune.fem.view import geometryGridView as geoGridView
from dune.fem.space import lagrange as solutionSpace
from dune.fem.scheme import galerkin as solutionScheme
def calculate(use_cpp, gridView):
# space on Gamma_0 to describe position of Gamma(t)
space = solutionSpace(gridView, dimRange=gridView.dimWorld, order=order)
u = TrialFunction(space)
v = TestFunction(space)
x = SpatialCoordinate(space.cell())
positions = space.interpolate(x, name="position")
# space for discrete solution on Gamma(t)
surface = geoGridView(positions)
space = solutionSpace(surface, dimRange=surface.dimWorld, order=order)
solution = space.interpolate(x, name="solution")
# set up model using theta scheme
theta = 0.5 # Crank-Nicolson
I = Identity(3)
dt = dune.ufl.Constant(0,"dt")
a = (inner(u - x, v) + dt * inner(theta*grad(u)
+ (1 - theta)*I, grad(v))) * dx
scheme = solutionScheme(a == 0, space, solver="cg")
Rexact = lambda t: numpy.sqrt(R0*R0 - 4.*t)
radius = switchCalcRadius(use_cpp,surface)
dt.value = 0.02
numberOfLoops = 3
times = numpy.zeros(numberOfLoops)
errors = numpy.zeros(numberOfLoops)
totalIterations = numpy.zeros(numberOfLoops, numpy.dtype(numpy.uint32))
gridSizes = numpy.zeros(numberOfLoops, numpy.dtype(numpy.uint32))
for i in range(numberOfLoops):
positions.interpolate(x * (R0/sqrt(dot(x,x))))
solution.interpolate(x)
t = 0.
error = abs(radius(surface)-Rexact(t))
iterations = 0
start = time.time()
while t < endTime:
info = scheme.solve(target=solution)
# move the surface
positions.assign(solution)
# store some information about the solution process
iterations += int( info["linear_iterations"] )
t += scheme.model.dt
error = max(error, abs(radius(surface)-Rexact(t)))
print("time used:", time.time() - start)
times[i] = time.time() - start
errors[i] = error
totalIterations[i] = iterations
gridSizes[i] = gridView.size(2)
if i < numberOfLoops - 1:
gridView.hierarchicalGrid.globalRefine(1)
dt.value /= 2
eocs = numpy.log(errors[0:][:numberOfLoops-1] / errors[1:]) / numpy.log(numpy.sqrt(2))
try:
import pandas as pd
keys = {'size': gridSizes, 'error': errors, "eoc": numpy.insert(eocs, 0, None), 'iterations': totalIterations}
table = pd.DataFrame(keys, index=range(numberOfLoops),columns=['size', 'error', 'eoc', 'iterations'])
print(table)
except ImportError:
print("pandas module not found so not showing table - ignored")
pass
return gridSizes, times
Compute the mean curvature flow evolution of a spherical surface. Compare computational time of a pure Python implementation and using a C++ algorithm to compute the radius of the surface for verifying the algorithm.
[4]:
# set up reference domain Gamma_0
results = []
from dune.alugrid import aluConformGrid as leafGridView
gridView = leafGridView("sphere.dgf", dimgrid=2, dimworld=3)
results += [calculate(True, gridView)]
gridView = leafGridView("sphere.dgf", dimgrid=2, dimworld=3)
results += [calculate(False, gridView)]
time used: 0.48349428176879883
time used: 2.5196492671966553
time used: 11.43457579612732
size error eoc iterations
0 318 0.001060 NaN 76
1 766 0.000605 1.619153 208
2 1745 0.000275 2.275142 420
time used: 0.6419370174407959
time used: 3.4394569396972656
time used: 14.355547189712524
size error eoc iterations
0 318 0.001060 NaN 76
1 766 0.000605 1.619153 208
2 1745 0.000275 2.275142 420
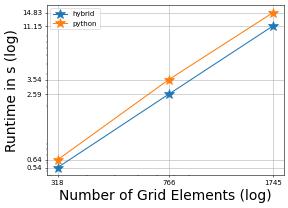
Compare the hybrid and pure Python versions
[5]:
plot(results[0],results[1])